2023+ Rumus Volume Tabung Serta Contoh Soal

Tahukah kamu rumus volume tabung? Untuk menghitung atau mencari volume tabung, maka kita menggunakan rumus. Para siswa siswi di sekolah, baik di SD, SMP, maupun SMA sering mendapatkan soal tentang volume tabung dari gurunya. Soal tersebut berisi pertanyaan tentang berapa volume yang dimiliki oleh sebuah tabung.

Volume Tabung

Berdasarkan hasil penelusuran kami, saat ini pencarian tentang rumus volume tabung sedang menduduki trend di google. Pencarian tersebut lebih banyak dilakukan oleh siswa siswi sekolah. Data tersebut menandakan bahwa saat ini mata pelajaran matematika mereka di sekolah telah sampai di pembelajaran bangun ruang, khususnya tabung.

Sebenarnya, penjelasan tentang rumus volume tabung telah banyak tersedia di internet. Tetapi, sebagian besar rumusnya tidak ditulis secara jelas sesuai dengan kaidah yang berlaku dalam penulisan persamaan matematika. Sepertinya, penulis terkendala dengan cara penulisan rumus matematika di blog.

Oleh karena itu, pada kesempatan kali ini, kami akan menjelaskan kembali rumus volume tabung untuk menyempurnakan materi-materi yang sebelumnya telah tersebar di internet. Selain itu, kami juga akan memberikan materi tambahan yang terkait dengan volume tabung. Semoga setelah membaca uraian ini, pengetahuan pembaca tentang rumus volume tabung semakin bertambah.

Baca Juga:

• Tabel Sin Cos Tan
• Rumus Keliling Lingkaran

Yuk, berikut ini ulasannya...

Tabung

Sebelum kita masuk pada pembahasan rumus volume tabung, ada baiknya terlebih dahulu kita perjelas kembali hakikat dari bangun ruang yang satu ini. Pengetahuan yang baik tentang tabung akan membantu kita memahami rumus-rumus yang terkait dengan tabung.

1. Pengertian Tabung

Tabung disebut juga dengan silinder. Dalam matematika geometri, tabung adalah bangun ruang tiga dimensi yang terbentuk dari dua lingkaran identik yang sejajar (sepusat) dan sebuah persegi panjang yang mengelilingi kedua lingkaran tersebut (kulit tabung).

Tabung atau silinder adalah bangun ruang yang mempunyai sisi atas (tutup) dan sisi bawah (alas) berbentuk lingkaran sejajar dan kongruen serta sisi lengkung yang merupakan selimut tabung. Tabung merupakan bangun ruang yang memiliki 3 sisi dan 2 rusuk.

2. Unsur atau Bagian Tabung

Adapun unsur atau bagian-bagian tabung (perhatikan gambar di atas) antara lain sebagai berikut:

1. Sisi atas (tutup), yaitu lingkaran dengan pusat L₁ dan sisi bawah (alas), yaitu lingkaran dengan pusat L₂
2. Sisi lengkung tabung (selimut tabung), yaitu daerah persegipanjang ABCD
3. Diameter lingkaran (d)
4. Jari-jari lingkaran, yaitu r₁ dan r₂ (r₁ = r₂ = r)
5. Tinggi tabung (t), yaitu jarak titik pusat L₁ dengan titik pusat L₂. AD = BC = t

3. Jaring-Jaring Tabung

Jaring-jaring tabung adalah pembelahan sebuah tabung dimana ketika bagian-bagian tersebut digabungkan akan membentuk tabung. Perhatikan gambar di bawah ini:

Gambar (a) memperlihatkan sebuah tabung dengan jari-jari r dan tinggi t. Apabila tabung pada gambar (a) diiris sepanjang garis tinggi (AD atau BC) dan sepanjang rusuk lengkung (sepanjang keliling lingkaran tutup dan sepanjang keliling lingkaran alas), dengan bentuk irisan seperti pada gambar (b).

Irisan tersebut akan menghasilkan jaring-jaring tabung seperti yang terlihat pada gambar (c). Jaring-jaring tabung terdiri dari sisi bawah (alas) dan sisi atas (tutup), keduanya merupakan lingkaran dengan jari-jari r. Sedangkan selimut tabung (sisi lengkung) adalah persegi panjang ABCD.

4. Permukaan Tabung

Permukaan tabung adalah bangun-bangun yang membatasi tabung. Luasnya dapat diketahui dengan melihat jaring-jaring tabung yang terdiri dari sisi atas (tutup), sisi bawah (alas), dan selimut tabung. Sehingga, luas permukaan tabung adalah luas seluruh jaring-jaring tersebut.

4.1. Luas Permukaan Tabung 

Luas permukaan tabung adalah gabungan dari luas selimut tabung, luas sisi atas (tutup), dan luas sisi bawah (alas). Luas selimut tabung sama dengan luas persegi panjang ABCD. Sementara itu, luas persegi panjang ABCD = panjang selimut tabung x lebar selimut tabung.

• Panjang selimut tabung (AB = DC) = keliling lingkaran sisi bawah (alas) atau keliling lingkaran lingkaran atas (tutup)
• Lebar selimut tabung (AD = BC) = tinggi tabung (t)
• Sehingga, luas selimut tabung = panjang selimut tabung x lebar selimut tabung = keliling lingkaran bawah atau atas (salah satunya) x tinggi tabung = 2πr x t (rumus luas selimut tabung)

Setelah mengetahui luas selimut tabung, selanjutnya kita bisa menentukan luas permukaan tabung yang dirumuskan sebagai berikut:
 

Luas Permukaan Tabung = luas selimut tabung + luas sisi alas (tutup) + luas sisi bawah (alas) = (2πr x t) + πr² + πr² = (2πr x t) + 2πr² = 2πr (t + r)

5. Rumus Volume Tabung

Dengan rumus volume tabung, maka kita bisa mengetahui daya tampung sebuah tabung saat diisi sesuatu. Begitupun sebaliknya, kita dapat mengetahui volume zat yang terdapat di dalam tabung, tanpa mengeluarkan zat tersebut dari tabungnya, misalnya minyak dalam drum.

5.1. Mencari Rumus Volume Tabung

Mencari besar volume sebuah tabung hampir sama dengan mencari volume prisma. Kedua bangun ruang ini memiliki kesamaan, yaitu memiliki dua bidang (sisi) sejajar yang kongruen (sama dan sebangun). Supaya lebih jelas, coba perhatikan gambar di bawah ini:

Dari gambar di atas, bisa kita pahami bahwa tabung adalah suatu prisma beraturan dengan segi yang sangat banyak. Apabila tutup prisma (alas prisma) segi beraturan seperti pada gambar di atas memiliki segi yang sangat banyak, maka bentuk tutup prisma akan mendekati bentuk lingkaran. Prisma yang memiliki bentuk tutup berupa lingkaran disebut tabung. Oleh karena itu, volume tabung dapat diperoleh dengan rumus:

Volume tabung = luas alas tabung x tinggi tabung = luas lingkaran x tinggi tabung = πr² x t = πr²t 

(r adalah jari-jari tabung dan t adalah tinggi tabung)

Contoh Soal Volume Tabung

Untuk membantu pemahaman pembaca tentang volume tabung, berikut ini beberapa contoh soal tentang volume tabung.

Contoh soal 1. Hitunglah volume tabung yang mempunyai jari-jari alas 7 cm dan tinggi 20 cm.

Jawaban:

Diketahui:

• r = 7 cm
• t = 20 cm

Ditanyakan:

• Volume tabung...?

Penyelesaian:

• Volume tabung = πr²t
• = ²² / ₇ x 7² x 20
• = 22 x 7 x 20
• = 3.080 cm³
  

Contoh Soal 2. Sebuah tabung terisi penuh dengan air sebanyak 5.024 cm³. Jari-jari alas tabung adalah 10 cm. Hitunglah tinggi air tersebut.

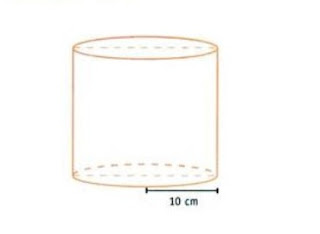
Jawaban: 

Diketahui:

• Volume tabung = 5.024 cm³
• r = 10 cm

Ditanyakan:

• t...?

Penyelesaian:

• Volume tabung = πr²t
• 5.024 = 3,14 x 10² x t
• 5.024 = 3,14 x 100 x t
• 5.024 = 314 x t
• t =  ^5.024 / ₃₁₄ 
• t = 16 cm

Contoh Soal 3. Sebuah kaleng makanan yang berbentuk tabung mempunyai tinggi 20 cm dan diameter 14 cm. Tentukan volume kaleng tersebut.

Jawaban:

Diketahui:

• t = 10 cm
• r = ^d / ₂ = ¹⁴ / ₂ = 7 cm

Ditanyakan:

• Volume kaleng (tabung)? 

Penyelesaian:

• Volume tabung = πr²t
• = ²² / ₇ x 7² x 20
• = 22 x 7 x 20
• = 3.080 cm³

Demikianlah penjelasan tentang Rumus Volume Tabung. Bagikan materi ini agar orang lain juga bisa membacanya. Terima kasih, semoga bermanfaat. 

2023+ Rumus Volume Tabung Serta Contoh Soal 2019-10-25T06:16:00-07:00 Rating: 4.5 Diposkan Oleh: Author Ilmusiana